AdamW 和 Super-convergence 现已成为训练神经网络最快的方式

技术
作者

Sylvain Gugger 和 Jeremy Howard

发布日期

2018年7月2日

Jeremy 的注释：欢迎来到 fast.ai 的第一位驻站学者，Sylvain Gugger。有什么比发布他在 fast.ai 的第一个研究项目的成果更好的方式来介绍他呢？我们将使用这项研究的成果来改变我们在下一版本课程和 fastai 库中训练模型的方式，这将使学生和实践者能够比以前的方法更可靠地更快地训练他们的模型。

Adam 的过山车之旅

Adam 优化器的发展历程堪称过山车。它于 2014 年首次提出，其核心思想简单直观：既然我们知道有些参数肯定需要比其他参数移动得更远更快，为什么还要对每个参数使用相同的学习率呢？由于最近梯度的平方告诉我们每个权重接收到的信号强度，我们可以直接除以它，以确保即使是最迟缓的权重也能有机会大放异彩。Adam 采纳了这个想法，在此基础上增加了标准的动量方法，然后（稍加调整以避免早期批次出现偏差）就完成了！

该方法刚发布时，深度学习社区看到原始论文中的图表（如下图所示）后，都充满了兴奋之情

Adam 与其他优化器的比较

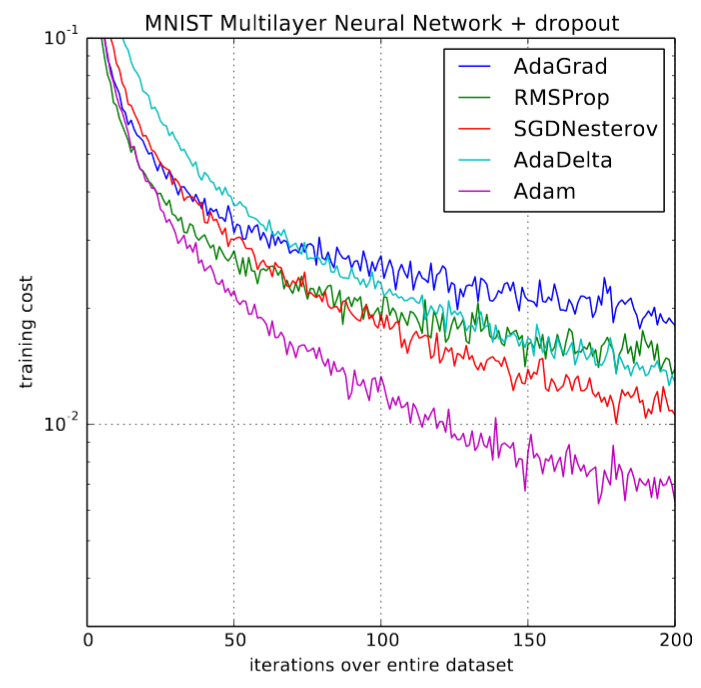
训练速度提升 200%！论文总结道：“总的来说，我们发现 Adam 鲁棒性强，非常适用于机器学习领域的各种非凸优化问题”。啊，是的，那些日子已是三年多前，在深度学习领域里，这就像是一辈子那么长。但很快就发现，事情并非如我们所愿。很少有研究论文使用它来训练模型，新的研究开始明确不鼓励使用它，并在多项实验中表明，普通的带动量的 SGD 表现更好。等到 2018 年 fast.ai 课程开始时，我们决定在早期课程中砍掉可怜的 Adam。

但在 2017 年底，Adam 似乎获得了新的生命力。Ilya Loshchilov 和 Frank Hutter 在他们的论文中指出，Adam 在每个库中的权重衰减实现方式似乎是错误的，并提出了一种简单的方法（他们称之为 AdamW）来修复它。虽然他们的结果略有混杂，但确实展示了一些令人鼓舞的图表，例如这张

Adam 与 AdamW 的比较

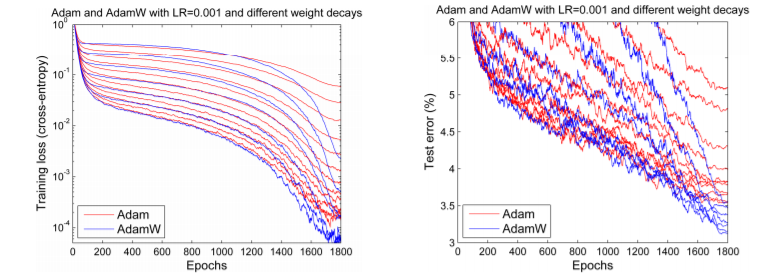
我们期待着 Adam 的热潮再次回归，因为似乎那些最初的结果或许可以再次实现。但这并没有发生。事实上，唯一实现了这个修复的深度学习框架是 fastai，使用了 Sylvain 编写的代码。由于缺乏广泛的框架支持，日常实践者只能继续使用旧的、“坏掉的” Adam。

但这还不是唯一的问题。更多障碍还在前面。另有两篇论文指出了可怜的 Adam 在收敛性证明中存在的明显问题，尽管其中一篇声称找到了修复方法（并在享有盛誉的 ICLR 会议上获得了“最佳论文”奖），他们称之为 amsgrad。但如果我们从这个关于这个最戏剧性生命（至少，以优化器标准来看算是戏剧性）的简短历史中学到了什么，那就是事情并非看起来那样简单。事实上，博士生 Jeremy Bernstein 指出，所谓的收敛问题实际上只是超参数选择不当的迹象，而且 amsgrad 可能根本无法解决问题。另一位博士生 Filip Korzeniowski 展示了一些似乎支持这种对 amsgrad 的不乐观观点的早期结果。

摆脱过山车

那么对于那些只想快速训练出准确模型的人来说，我们该怎么办？让我们用几百年来解决科学争论的相同方式来解决这场争论：通过实验！我们稍后会告诉你所有细节，但首先，这里是结果摘要

  • 正确调优后，Adam 确实有效！我们在各种任务上取得了新的 SOTA (State-of-the-art，最先进) 结果（在训练时间方面），例如
    • 在 DAWNBench 竞赛中，使用测试时增强 (Test Time Augmentation) 只需 18 个 epoch 或不使用测试时增强只需 30 个 epoch，即可将 CIFAR10 训练到 >94% 的准确率；
    • 仅用 60 个 epoch 即可在 Cars Stanford 数据集上将 Resnet50 微调到 90% 准确率（之前的报告达到相同准确率需要 600 个 epoch）；
    • 从头训练 AWD LSTM 或 QRNN，在 Wikitext-2 上用 90 个 epoch（或在单 GPU 上用 1.5 小时）达到 SOTA 的困惑度（之前的报告中 LSTM 使用 750 个 epoch，QRNN 使用 500 个 epoch）。
  • 这意味着我们（据我们所知，首次）使用 Adam 实现了超收敛！超收敛是一种现象，发生在以高学习率训练神经网络时，在训练的前半段学习率会增长。在理解超收敛之前，将 CIFAR10 训练到 94% 准确率大约需要 100 个 epoch。
  • 与之前的工作相反，我们看到 Adam 在我们尝试过的所有 CNN 图像问题上都能达到与 SGD+Momentum 差不多的准确率，只要它经过适当调优，而且它几乎总是稍微快一些。
  • 关于 amsgrad 是一个糟糕的“修复”的说法是正确的。我们持续发现 amsgrad 相对于普通的 Adam/AdamW 在准确率（或其他相关指标）上没有任何提升。

当你听到有人说 Adam 不如 SGD+Momentum 泛化得好时，你几乎总是会发现他们为模型选择了糟糕的超参数。Adam 通常比 SGD 需要更多的正则化，因此在从 SGD 切换到 Adam 时，请务必调整你的正则化超参数。

以下是本文其余部分的概述

  1. AdamW
    1. 理解 AdamW
    2. 实现 AdamW
    3. AdamW 实验结果
  2. amsgrad
    1. 理解 amsgrad
    2. 实现 amsgrad
    3. amsgrad 实验结果
  3. 完整结果表格

AdamW

理解 AdamW：权重衰减还是 L2 正则化？

L2 正则化是一种减少过拟合的经典方法，它包括将模型所有权重的平方和添加到损失函数中，并乘以给定的超参数（本文所有公式均使用 python、numpy 和 pytorch 符号表示）

final_loss = loss + wd * all_weights.pow(2).sum() / 2

…其中 wd 是需要设置的超参数。这也称为权重衰减，因为在应用普通 SGD 时，它等价于像这样更新权重

w = w - lr * w.grad - lr * wd * w

（注意，w2 对 w 的导数是 2w。）在这个公式中，我们看到我们如何在每一步都减去权重的一小部分，因此得名衰减。

我们查看过的所有库都使用了这两种形式中的第一种。（实际上，它几乎总是通过将 wd*w 添加到梯度中来实现，而不是真正修改损失函数：当有更简单的方法时，我们不想通过修改损失函数来增加计算量。）

那么，如果这两个概念是同一回事，为什么要区分它们呢？答案是，它们只对普通 SGD 来说是同一回事，但只要我们加入动量，或使用像 Adam 这样更复杂的优化器，L2 正则化（第一个公式）和权重衰减（第二个公式）就会变得不同。在本文的其余部分，当我们谈到权重衰减时，我们将始终指代第二个公式（将权重稍微衰减一点），如果想提及经典方法，则会谈到 L2 正则化。

例如，我们来看看带动量的 SGD。使用 L2 正则化包括将 wd*w 添加到梯度中（正如我们之前看到的），但梯度不是直接从权重中减去的。首先我们计算一个移动平均值

moving_avg = alpha * moving_avg + (1-alpha) * (w.grad + wd*w)

…正是这个移动平均值将乘以学习率并从 w 中减去。因此，与正则化相关、将从 w 中提取的部分是 lr* (1-alpha)*wd * w，再加上之前已经在 moving_avg 中的权重的组合。

另一方面，权重衰减的更新将如下所示

moving_avg = alpha * moving_avg + (1-alpha) * w.grad 
w = w - lr * moving_avg - lr * wd * w

我们可以看到，从 w 中减去的与正则化相关的部分在这两种方法中是不同的。当使用 Adam 优化器时，差异就更大了：在使用 L2 正则化的情况下，我们将 wd*w 添加到梯度中，然后计算梯度及其平方的移动平均值，再将两者用于更新。而权重衰减方法则只是进行更新，然后从每个权重中减去。

显然，这是两种不同的方法。经过实验，Ilya Loshchilov 和 Frank Hutter 在他们的文章中建议，我们应该将权重衰减与 Adam 结合使用，而不是经典深度学习库实现的 L2 正则化。

实现 AdamW

我们如何做到这一点？如果您使用 fastai 库，这会非常容易，因为它已经内置实现。具体来说，如果您使用 fit 函数，只需添加参数 use_wd_sched=True

learn.fit(lr, 1, wds=1e-4, use_wd_sched=True)

如果您更喜欢新的训练 API，您可以在每个训练阶段使用参数 wd_loss=False（表示权重衰减不在损失中计算）

phases = [TrainingPhase(1, optim.Adam, lr, wds=1-e4, wd_loss=False)]
learn.fit_opt_sched(phases)

以下是我们如何在 fastai 中实现此功能的快速摘要。在优化器的 step 函数内部，仅使用梯度来修改参数，参数本身的值完全不被使用（除了权重衰减，但我们将在外部处理它）。然后，我们可以在优化器 step 之前简单地执行权重衰减。这仍然需要在计算梯度之后完成（否则会影响梯度值），因此在您的训练循环中，您必须找到这个位置。

loss.backward()
#Do the weight decay here!
optimizer.step()

当然，优化器应该设置 wd=0，否则它会进行一些 L2 正则化，这正是我们目前不想要的。现在在这个位置，我们必须遍历所有参数并进行我们的小权重衰减更新。您的参数都应该在优化器的 param_groups 字典中，因此循环看起来像这样

loss.backward()
for group in optimizer.param_groups():
    for param in group['params']:
        param.data = param.data.add(-wd * group['lr'], param.data)
optimizer.step()

AdamW 实验结果：有效吗？

我们在计算机视觉问题上的首次测试非常令人鼓舞。具体来说，我们使用 Adam 和 L2 正则化，在 30 个 epoch 内（这是 SGD 在使用1cycle 策略达到 94% 准确率所需的时间）达到的准确率平均为 93.96%，有一半的几率超过 94%。而使用 Adam 和权重衰减，我们稳定地达到了 94% 到 94.25% 之间的准确率。为此，我们发现在使用 1cycle 策略时，beta2 的最优值为 0.99。我们将 beta1 参数视为 SGD 中的动量（这意味着随着学习率的增长，它从 0.95 变为 0.85，然后当学习率降低时，它再回到 0.95）。

使用 L2 正则化或权重衰减的准确率

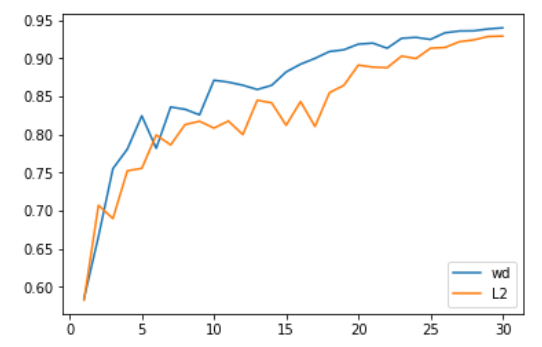
更令人印象深刻的是，使用测试时增强（即对测试集的一张图片及其四个数据增强版本的预测进行平均），我们仅用 18 个 epoch 就能达到 94% 的准确率（平均 93.98%）！而使用普通的 Adam 和 L2 正则化，每二十次尝试中只有一次能超过 94%。

在这些比较中需要考虑的一点是，改变正则化方式会改变权重衰减或学习率的最佳值。在我们进行的测试中，使用 L2 正则化时最佳学习率为 1e-6（最大学习率为 1e-3），而权重衰减的最佳值为 0.3（学习率为 3e-3）。数量级上的差异在我们所有测试中都非常一致，主要源于 L2 正则化实际上被梯度的平均范数（相当低）有效除以，并且 Adam 的学习率相当小（因此权重衰减的更新需要更强的系数）。

那么，使用 Adam 时，权重衰减是否总是比 L2 正则化更好呢？我们还没有发现它明显更差的情况，但对于迁移学习问题（例如在 Stanford cars 数据集上微调 Resnet50）或 RNN，它并没有带来更好的结果。

amsgrad

理解 amsgrad

Amsgrad 是 Sashank J. Reddi、Satyen Kale 和 Sanjiv Kumar 在最近的一篇文章中提出的。通过分析 Adam 优化器的收敛性证明，他们发现更新规则中存在一个可能导致算法收敛到次优点的错误。他们设计了理论实验，展示了 Adam 可能失败的情况，并提出了一个简单的修复方法。

为了理解这个错误和修复方法，我们来看看 Adam 的更新规则（如果你需要复习，Sebastian 的文章很不错）

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad
avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)
w = w - lr * avg_grads / sqrt(avg_squared)

我们跳过了偏置校正（在训练初期有用），以便专注于重点。作者在 Adam 证明中发现的错误在于，它要求以下量

lr / sqrt(avg_squared)

…这是我们在平均梯度方向上迈出的步长，需要在训练过程中递减。由于学习率通常是常数或递减的（除了像我们这样试图实现超收敛的“疯子”），作者提出的修复方法是强制 avg_squared 量增加，通过添加另一个变量来跟踪它们的最大值。

实现 amsgrad

这篇相关文章在 ICLR 2018 上获奖，并获得了很高的人气，目前已在两个主要的深度学习库 pytorch 和 Keras 中实现。只需将选项设置为 amsgrad=True 即可启用，操作很简单。

这将导致前一节中的权重更新代码更改为如下所示

avg_grads = beta1 * avg_grads + (1-beta1) * w.grad
avg_squared = beta2 * (avg_squared) + (1-beta2) * (w.grad ** 2)
max_squared = max(avg_squared, max_squared)
w = w - lr * avg_grads / sqrt(max_squared)

amsgrad 实验结果：很多噪音，毫无用处

Amsgrad 结果非常令人失望。在我们的所有实验中，我们都没有发现它有任何帮助，即使 amsgrad 找到的最小值（就损失而言）有时确实比 Adam 达到的最小值略低，但指标（准确率、f1 分数等）总是更差（参见引言中的表格，或此处的更多示例）

Adam 优化器在深度学习中的收敛性证明（因为它针对的是凸问题）以及他们在其中发现的错误，只对与实际问题无关的合成实验有意义。实际测试表明，当这些 avg_squared 梯度想要减小时，这样做对于最终结果是最好的。

这表明，即使专注于理论有助于获得一些新想法，但要想确保这些想法真正帮助实践者训练出更好的模型，没有任何东西可以替代实验（而且是大量的实验！）

附录：完整结果

从头训练 CIFAR10（模型为 wide resnet 22，显示五种模型的测试集平均误差）

方法 不使用 amsgrad 使用 amsgrad
AdamW 5.66% 6.31%
Adam 6.06% 6.64%

使用 fastai 库引入的标准头部在 Stanford Cars 数据集上微调 Resnet50（先训练头部 20 个 epoch，然后解冻并使用差异化学习率训练 40 个 epoch）。

方法 不使用 amsgrad 使用 amsgrad
AdamW 10.8%/9.5% 10.1%/9.5%
Adam 10.4%/9% 10.1%/9%

使用 github 仓库中的超参数训练 AWD LSTM（结果显示验证集/测试集上的困惑度，使用或不使用缓存指针）

方法 原始模型 使用缓存指针
Adam 68.7/65.5 52.9/50.9
Adam + amsgrad 69.4/66.5 53.1/51.3
AdamW 68.9/65.7 52.8/50.9
AdamW + amsgrad 72.7/69 57/54.7

使用 QRNN 代替 LSTM 的情况相同

方法 原始模型 使用缓存指针
Adam 69.6/66.7 53.6/51.7
Adam + amsgrad 71.5/68.4 54.2/52.2
AdamW 70.5/67.3 55.5/53.3
AdamW + amsgrad 74.3/70.9 57.8/55.6

对于这个特定任务，我们使用了修改过的 1cycle 策略，更快地增加学习率，然后保持长时间的高常数学习率，最后再下降。

Adam 与其他优化器的比较

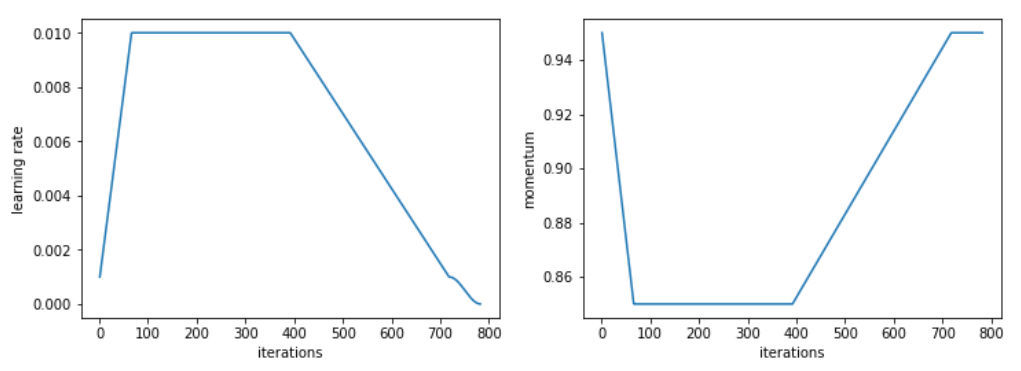
所有相关超参数的值以及用于生成这些结果的代码可在此处获取。