概述
从随机分布生成数字是一个任何程序员都可能在某个时候需要的实用工具。C++11 增加了丰富多样的随机分布生成功能。这使得使用随机分布变得简单快速,不仅在使用 C++11 时如此,而且在使用任何允许与 C++ 互操作的语言时也是如此。
在本文中,我们将学习随机分布的用途、如何生成它们以及如何在 C++11 中使用它们。我还会展示如何通过将 C++11 的类封装为 Swift 类,从而为 Swift 创建新的随机分布功能。虽然 Swift 不直接支持 C++,但我将展示如何通过为 C++ 类创建纯 C 封装来解决这个问题。
随机分布及其重要性
如果像负二项分布和泊松分布这样的名称只是你很久以前学过的一些东西的模糊记忆,请给我点时间,让我尝试说服你,随机分布的世界值得你投入时间和精力。
程序员已经知道随机数的概念。但对许多人来说,我们的工具箱仅限于均匀实数随机数和整数随机数,偶尔可能还会用到一些高斯(正态)随机数。生成随机数的方法还有很多!事实上,你甚至可能在不知不觉中重新实现了标准的随机分布……
例如,假设你正在编写一个音乐播放器,用户对各种歌曲进行了从一星到五星的评分。你想实现一个“随机播放”功能,它会随机选择歌曲,但更频繁地选择评分较高的歌曲。你会如何实现呢?答案是:使用随机分布!更具体地说,你需要来自*离散分布*的随机数;也就是说,使用一组权重生成一个随机整数,权重较高的数字被按比例选择的频率更高。
或者你可能正试图模拟向系统添加更多资源后预测的队列长度。你模拟这个过程,因为你想知道的不仅仅是平均队列长度,还包括它大于某个大小的频率、95百分位数大小是多少等等。你不确定系统的一些输入是什么,但你知道可能值的范围,并且对你认为最可能的值有一个猜测。在这种情况下,你需要来自*三角分布*的随机数;也就是说,生成一个随机浮点数,它通常接近你的猜测值,并且离猜测值越远可能性呈线性下降,超出可能值范围时概率降至零。(这种模拟构成了概率编程的基础。)
还有几十种其他的随机分布,包括
- 经验分布:从历史数据中随机选择一个数字
- 负二项分布:在指定次数的失败发生之前成功的次数
- 泊松分布:可用于建模固定时间段内以固定频率发生的独立事件的数量
如何生成随机分布
通常,从某种随机分布生成数字的步骤是
- 为你的生成器设置种子
- 使用生成器生成下一批随机位
- 将这些随机位转换为你选择的分布
- 如果需要更多随机数,回到步骤 (2)
我们通常所说的“随机数生成”实际上是步骤 (2):使用伪随机生成器,它确定性地生成一系列尽可能看起来“随机”的数字(即彼此不相关、分布均匀等)。伪随机生成器是具有这些属性的某个函数,例如梅森缠绕器。要开始生成序列,你需要一个*种子*;也就是说,传递给生成器的第一个数字。大多数操作系统都有生成随机种子的方法,例如 Linux 和 Mac 上的/dev/random,它使用环境输入(如设备驱动程序的噪声)来获取一个应该是真正随机的数字。
然后在步骤 3 中,我们将伪随机生成器创建的随机位转换为具有所需分布的东西。有一些普遍适用的方法,例如逆变换采样,它可以将均匀随机数转换为任何给定的分布。也有针对特定分布的更快的方法,例如Box-Muller 变换,它可以从均匀生成器创建高斯(正态)随机数。
要生成更多随机数,你无需返回使用 /dev/random,因为现在你已经设置好了一个伪随机生成器。相反,你只需从你的生成器中获取下一个数字(步骤 (2)),然后将其传递给你生成分布的转换(步骤 (3))。
这在 C++ 中如何工作
C++11 在标准库头文件 <random> 中包含了上述每个步骤的功能。步骤 (1) 只需创建一个 random_device 即可实现(本文中我没有包含 std:: 前缀;你可以输入 std::random_device 或在 C++ 文件顶部添加 using namespace std)。然后将此对象传递给提供的各种伪随机生成器之一的构造函数,例如 mt19937,它就是梅森缠绕器生成器;这就是步骤 (2)。接着,使用适当的类(如 discrete_distribution)构造一个随机分布对象,并传入该分布所需的任何参数(例如,对于 discrete_distribution,你传入每个可能值的权重列表)。最后,调用该对象(它支持 () 运算符,因此它是一个 functor,在 Python 中称为 callable),并传入你创建的伪随机生成器。这是来自优秀网站 cppreference.com 的一个完整示例。
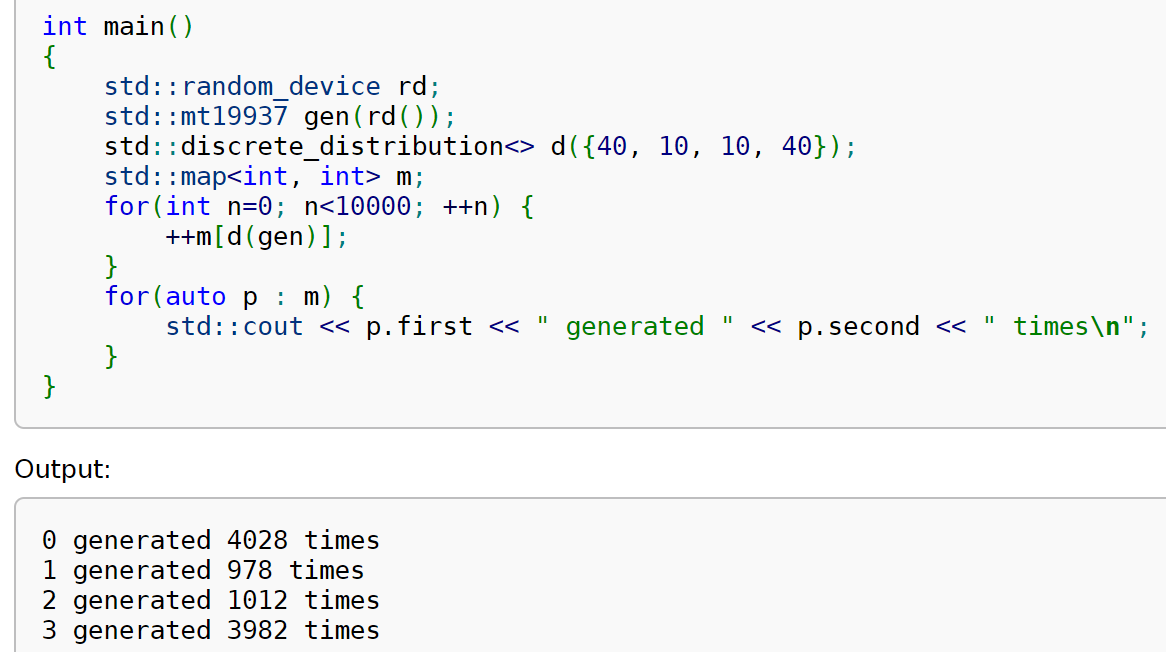
如果你曾认为 C++ 代码总是冗长而复杂,这个示例可能会让你重新思考你的假设!正如你所见,每个步骤都与上一节中描述的随机分布过程概述很好地对应。(顺便说一句:如果你对学习现代 C++ 感兴趣,cppreference.com 拥有一个非凡的集合,包含了 C++ 标准库每个部分的精心设计的示例;这可能是学习如何有效实践使用该语言的最佳场所。你甚至可以在线编辑和运行这些示例!)
C++11 提供的分布有
- 整数生成:
uniform_int_distribution,binomial_distribution,negative_binomial_distribution,geometric_distribution,poisson_distribution - 实数生成:
uniform_real_distribution,exponential_distribution,gamma_distribution,weibull_distribution,normal_distribution,lognormal_distribution,chi_squared_distribution,cauchy_distribution,fisher_f_distribution,student_t_distribution - 布尔值生成:
bernoulli_distribution
这在 Swift 中如何工作
虽然 Swift 4 现在提供了一些基本的随机数支持,但它仍然不提供任何非均匀分布。因此,我已经将所有 C++11 随机分布通过我的BaseMath库提供给了 Swift。有关我创建此库的原因和方法的更多信息,请参阅使用 Swift 进行高性能数值编程。我稍后会展示如何构建这个封装,但首先让我们看看如何使用它。这是我们在 C++ 中看到的相同函数,转换为 Swift+BaseMath 后是这样的
let arr = Int.discrete_distribution([40, 10, 10, 40])[10000]
let counts = arr.reduce(into: [:]) { $0[$1, default:0] += 1 }
counts.sorted(by:<).forEach { print("\($0) generated \($1) times") }如你所见,在 Swift 中使用 BaseMath 生成随机数可以简化为:Int.discrete_distribution([40, 10, 10, 40])[10000]。我们可以比 C++11 更简洁地做到这一点,因为我们没有暴露那么多选项和细节。BaseMath 简单地假设你想使用标准的种子化方法,并使用 mt19937 梅森缠绕器生成器。
BaseMath 中的分布名称与 C++11 中完全相同,你只需在每个名称前加上你想要生成的类型(整数分布使用 Int 或 Int32,实数分布使用 Double 或 Float)。每个分布都有一个 init 方法,其名称和类型与 C++11 分布构造函数匹配。这会返回一个具有多个方法的 Swift 对象。正如前面讨论的,C++11 对象提供了 ()(*函数对象*)运算符,但不幸的是,Swift 中不能重载这个运算符。因此,我们借用了 Swift 的 subscript 特殊方法来获得等效的行为。唯一的区别是我们需要使用 [] 而不是 ()。如果你使用空的下标 [],BaseMath 将返回一个随机数;如果你使用一个 Int,例如 [10000],BaseMath 将返回一个数组。(也有生成缓冲区指针和对齐存储的方法。)初次使用 subscript 而不是函数对象可能会觉得有点奇怪,但这是一种完全足以绕过 Swift 限制的方法。我将把这称为*准函数对象*;也就是说,它的行为类似于函数对象,但使用 [...] 调用。
使用 Swift 封装 C++
为了使 C++11 随机分布在 Swift 中可用,我需要做两件事
- 在 C API 中封装 C++ 类,因为 Swift 不能直接与 C++ 互操作
- 使用 Swift 类封装 C API
我们将依次介绍每个步骤
在 C 中封装 C++ 类
C 封装代码在CBaseMath.cpp中。mt19937 梅森缠绕器生成器将被封装在一个名为 RandGen 的 Swift 类中,因此封装这个类的 C 函数都带有 RandGen_ 前缀。以下是 C 封装器的代码(请注意,封装器内部可以使用 C++ 特性,只要头文件中的接口是纯 C):
struct RandGenC:mt19937 {};
typedef struct RandGenC RandGenC;
RandGenC* RandGen_create() {
return (RandGenC*)(new mt19937(random_device()()));
}
void RandGen_destroy(RandGenC* v) {
delete(v);
}我们封装的每个类的模式都将与此类似。我们至少会有
- 一个派生自要封装的 C++ 类的
struct(struct RandGenC),以及一个 typedef,允许我们直接使用这个名称。通过使用 struct 而不是void*,我们可以直接在 C++ 中调用方法,但可以从我们的纯 C 头文件中隐藏模板和其他 C++ 内部细节。 - 一个
_create函数,它构造该类的一个对象并返回指向它的指针,并将其强制转换为我们的 struct 类型。 - 一个
_destroy函数,用于删除该对象。
在我们的头文件中,将列出每个函数以及 typedef。任何导入此 C API 的代码,包括我们的 Swift 代码,实际上都不会知道 struct 实际包含什么,因此我们将无法直接使用该类型(因为头文件中未提供其大小和布局)。相反,在使用此 API 的代码中,我们将仅使用不透明指针。
以下是封装分布的代码;看起来几乎一样
struct uniform_int_distribution_intC:uniform_int_distribution<int> {};
typedef struct uniform_int_distribution_intC uniform_int_distribution_intC;
uniform_int_distribution_intC* uniform_int_distribution_int_create(int a,int b) {
return (uniform_int_distribution_intC*)(new uniform_int_distribution<int>(a,b));
}
void uniform_int_distribution_int_destroy(uniform_int_distribution_intC* v) {
delete(v);
}
int uniform_int_distribution_int_call(uniform_int_distribution_intC* p, RandGenC* g) {
return (*p)(*g);
}主要区别在于增加了一个 _call 函数,以便我们实际调用方法。此外,由于类型是模板化的,我们必须为每个要支持的模板类型创建单独的封装集;上面显示了 <int> 的示例。请注意,由于 C 不支持重载,这个类型需要包含在每个函数的名称中。
当然,这一切看起来相当冗长,我们肯定不想为每个分布都手工写出来。所以我们不会!相反,我们使用gyb模板为我们创建它们,并自动生成头文件。如果时间允许,我们将来会更详细地探讨这一点。但现在,你可以查看模板的源代码。
在 Swift 中封装 C API
现在我们有了 C API,我们可以轻松地在 Swift 中重新创建原始的 C++ 类,例如
public class RandGen {
public let ptr:OpaquePointer?
public init() { ptr=RandGen_create() }
deinit { RandGen_destroy(ptr) }
}如你所见,我们在 init 中调用我们的 _create 函数,在 deinit 中调用 _destroy。正如前一节讨论的,我们的 C API 用户不了解我们的 struct 的内部细节,因此 Swift 只会给我们一个 OpaquePointer。
我们为每个分布创建类似的封装器(它们也定义了 subscript,它将调用我们的 _call 函数),此外还通过适当的静态封装器扩展了数值类型,例如
extension Int32 {
public static func uniform_int_distribution(_ g_:RandGen, _ a:Int32, _ b:Int32)
-> uniform_int_distribution_Int32 {
return uniform_int_distribution_Int32(g_, a,b)
}
}线程安全的生成器
必须构造并传入一个 RandGen 对象不太方便,特别是当我们必须处理线程安全的复杂性时。C++ 库通常不是线程安全的;这也包括 C++11 随机生成器。因此,我们必须小心不要在线程之间共享同一个 RandGen 对象。正如我在上一篇*使用 Swift 进行高性能数值编程*文章中讨论的那样,我们可以通过使用*线程局部存储*轻松获得线程安全的对象。我将此属性添加到了 RandGen
static var stored:RandGen {
if let r = Thread.current.threadDictionary["RandGen"] as? RandGen { return r }
return Thread.setToTLS(RandGen(), "RandGen")
}这使得我们可以向每个分布类添加以下版本的函数,从而让用户无需考虑创建或使用 RandGen 类。
public convenience init(_ a:Int32, _ b:Int32) {
self.init(RandGen.stored, a,b)
} 使用协议和 BaseMath 的扩展
上述步骤使我们具备了每次生成单个随机数的功能。为了生成一个集合,我们可以添加一个 Distribution 协议,每个分布都遵循该协议,并按如下方式扩展它
public protocol Distribution:Nullary {
subscript()->Element {get}
subscript(n:Int)->[Element] {get}
}
extension Distribution {
public subscript(n:Int)->[Element] {
return [Element].fill(self, n)
}
}如你所见,我们利用了 BaseMath 的方法 fill,它会调用一个函数或准函数对象 n 次,并返回一个新的 BaseVector(在本例中是一个 Array),其中包含每次调用的结果。
你可能想知道上面提到的 Nullary 协议。你可能已经听说过*一元*(带一个参数的函数或运算符)、*二元*(带两个参数)和*三元*);不太为人所知但同样有用的是术语*零元*,它只是一个不带参数的函数或运算符。如前所述,Swift 不支持重载 () 运算符,因此我们使用 subscript 添加了一个 Nullary 协议
public protocol Nullary {
associatedtype Element:SignedNumeric
subscript()->Element {get}
}试一试!
如果你是一名 C++ 或 Swift 程序员,不妨试试其中的一些随机分布——或许你甚至可以尝试创建一些模拟并进入概率编程的世界!或者如果你是一名 Swift 程序员,想使用 C++ 库中的功能,可以尝试用符合 Swift 习惯的 API 封装它,并将其作为 Swift 包提供给任何人使用。